Lingze's blog
lingze
2022-02-09
目录

lexical analysis

# lexical analysis

# 综述

词法分析是编译过程的第一步，主要是从输入的字符串识别出token，

# token

一个token对应句子不可再分割的一串字符串，类似英语单词， 一个token class对应一个字符串。

常见的token如：

  • 标识符， 变量名、函数名、类名等。
  • 常数
  • 关键字
  • ....

词法分析的设计：

  • 定义有限个数的token
  • 设置对于各个token对应的字符串

一般一个token由两部分组成：

  • 一个特殊的字符串表示token
  • 词素 lexeme， 即这个token表示对象的意义(数值)。

词法分析器产生的就是一对 token-lexeme 数据。

当然可能还有行号文件名等报错信息。

# 语法分析的实现

# 线性扫描

就是直接从左向右依次跑过来，遇到字符以后进行初步判断，然后继续向下。。

这种处理方式适合token不多而且不复杂的情况，实现起来比较简单，

线性扫描会容易遇到的问题就是在很多情况下需要进行向前的试探， 因为可能很多数值最开始是一样的，

一个比较简单的线性扫描器的实现就是json parser， 直接一次跑完即可， 遇到{则认为是object， 遇到"认为是string， 但是对于false\true等需要进行往后几个字符的试探，才能判断具体是哪个。

# 正则匹配

一些表示符:

  • union 表示或
    • A+B = A|B
  • Range:
    • 'a'+'b'+...+'z' = [a-z]
  • excluded range
    • Complement of [a-z] = [^a-z]
  • * 匹配0-多次
  • ?匹配0/1次
  • +匹配1-多次

# 实现

  • 对每个token编写对应的正则语法。
  • 集合R， 包含所有token对应的正则
  • 输入: x1--xn, 判断x1--xi 是否属于 R,
  • 如果属于的话，我们将得到对应的Ri， 即对应的token，
  • 移除x1--xi， 回到第三部继续判断，直到结束。

# 歧义

可能出现的问题：

  • 同时命中
    • 则选择长度最大的
  • 同时命中+长度一致
    • 则按照定义表达式的先后顺序，选择先定义的。

# 错误处理

如果出现了不可被识别的输入，

在最后设置一个所有错误字符串的定义，并进行报错，

# 对比

输入是依次的，即一个个字符，

在线性扫描器中，从开始输入，随着输入的继续会尝试判断选择token， 这个过程会比较繁琐，而且实现后不好拓展， 在某些情况下还要进行回退/前瞻等操作。

在正则匹配的实现中，输入以后会依次选择每个token对应的表达式，并判断是否命中，最后整理匹配到的表达式，并按照最长和优先定义的方案进行选择，然后返回对应表达式，这种方案有利于拓展。

# 语言和编译的定义

首先， 编译原理和语言学的理论基础是集合论。

  • 字母表 ∑

    • 字母表计时一个有限元素的集合
    • 其中的每个元素称为符号

  • ∑上的句子 s sentences

    • 句子就是一串符号， 其中的每一个符号都是属于∑的， 句子用s表示
      • 句子可以看作符号的集合，且句子是字母表的子集。

  • 𝜺 epsilon, 空句子

    • 表示没有任何符号的句子, epsilon, 空句子也是一个句子。这个其实是集合的空集

  • 语言 L language

    • 一个语言就是句子合集，任何一个句子集合都可以称为语言。

  • 编译 compile

    • 给定两个语言， Ls, Lo, 和一个句子ss, 判断ss是否属于Ls, 并在Lo中找到句子so， 保证so和ss意义相同。

# finite automata

有限状态机， 正则就是基于有限状态机实现的。

# overview

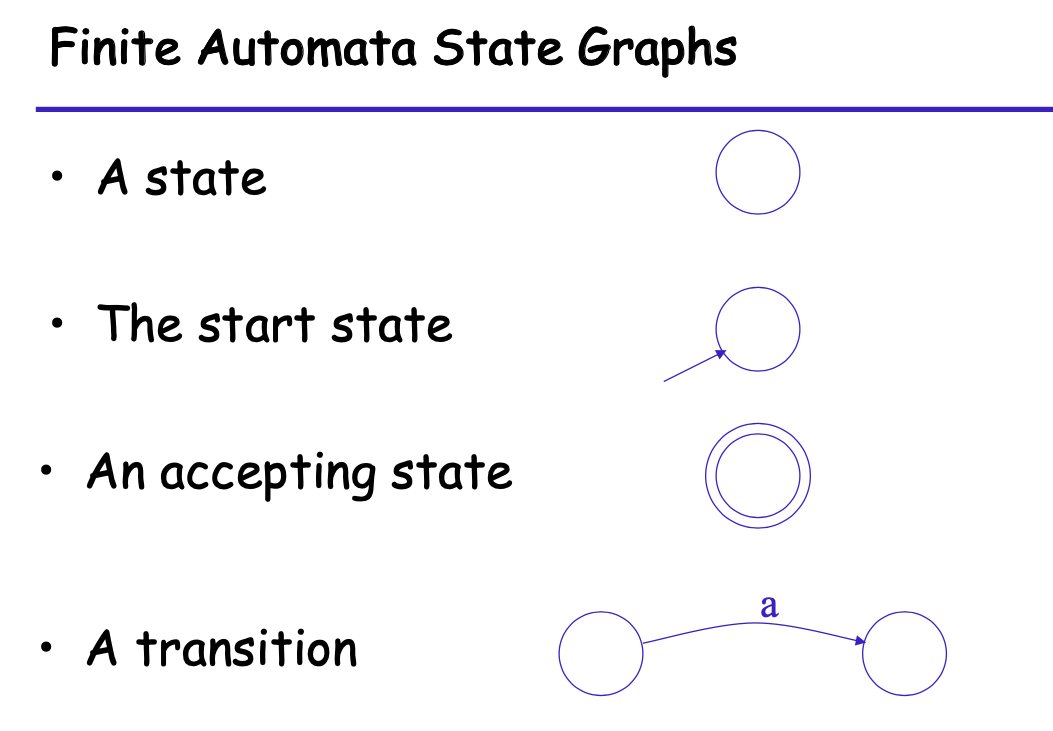
有限状态机包含一下五个部分：

  • 输入符号表，∑，
  • 状态集合 S
  • 起始状态 n
  • 终止状态 接受状态 F，
  • 转移函数

有限状态机的运行：

  • 一开始在起始状态n，
  • 不断的读取数据，并随着输入进行状态变化，
  • 如果最后的状态为接受状态， 那么表示接受本次输入。
  • 如果最后状态不是接受状态，那么表示拒接本次输入。

# FA图

image.png

# NFA & DFA

Deterministic Finite Automata

确定状态有限状态机

  • 对于每一次输入都会有一次状态改变，

  • 没有epsilon-moves

Nodeterministic Finite Automata

不确定状态有限状态机，

  • 对于每次输入都可以有0、1、多次状态转换，
  • 可以epsilon-moves

# epsilon moves

一种特殊的状态转换，只存在于NFA中，是指不接收任何符号，可以直接进行状态切换，

epsilon是一个特殊的句子，表示没有任何符号的句子 (空集)

# FA的执行

在FA图中， DFA每次输入只能进行一个路径。

  • 由输入决定其复杂程度

在NFA中， 可以选择：

  • 是否进行epsilon-moves
  • 选择某一次输入对应的多个转换中的哪个
    • NFA会尽可能选择可以到达终结状态的路径

# NFA vs DFA

在表示同样的正则表达式时，

  • DFA运行的更快速
    • 因为不需要进行路径选择
  • NFA更加简洁
    • DFA可以指数级别的大于NFA

# 从正则表达式转化成有限状态机

简述

  • 语法描述
  • 正则表达式
  • NFA
  • DFA
  • 表驱动实现的DFA

# 正则到NFA

其实是一套直接对应的转换了

首先对于一个表达是M， 我们写为一个大圆弧形式

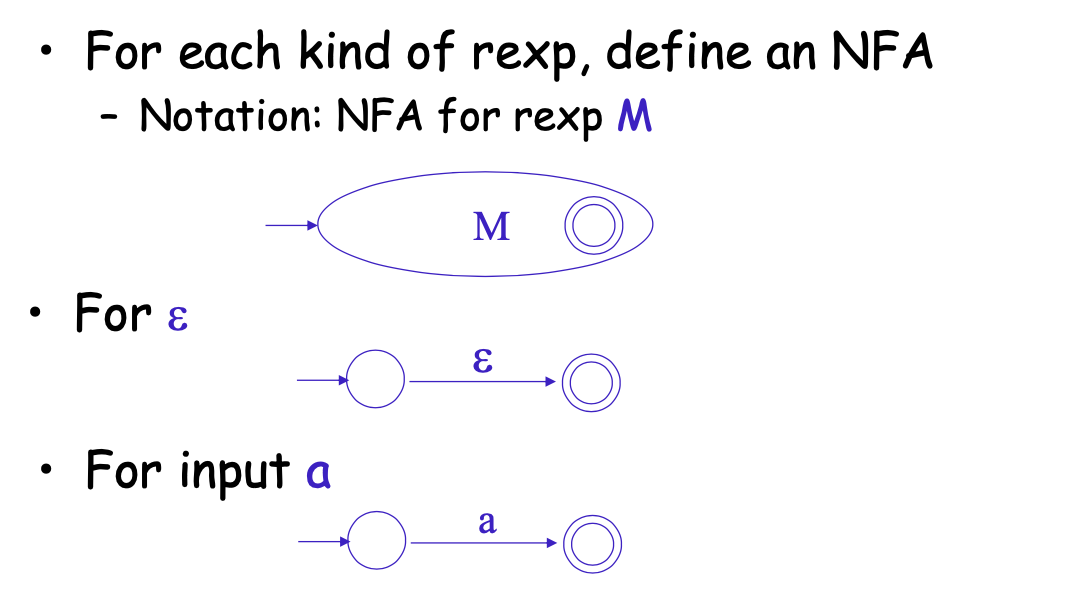
image.png

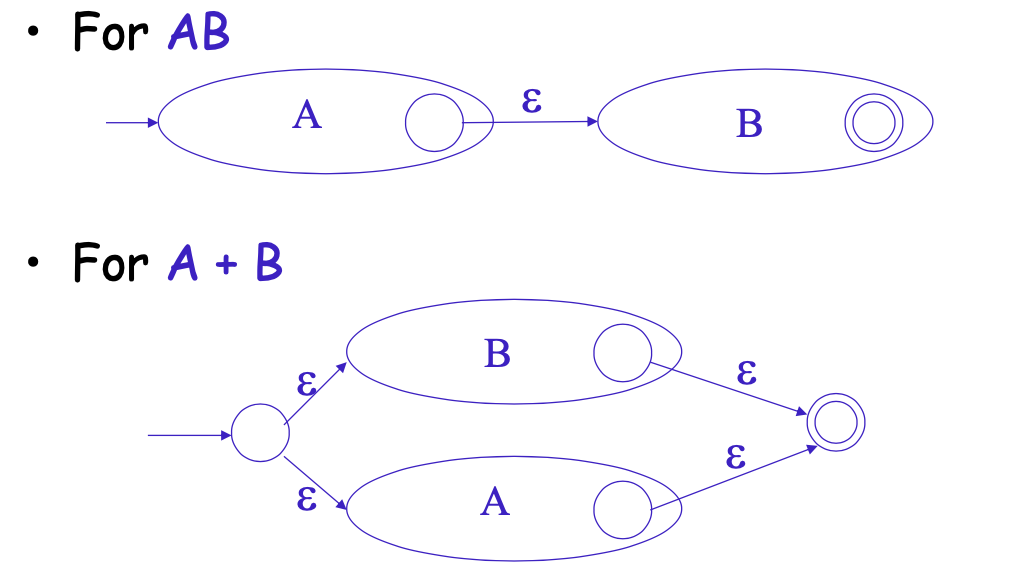
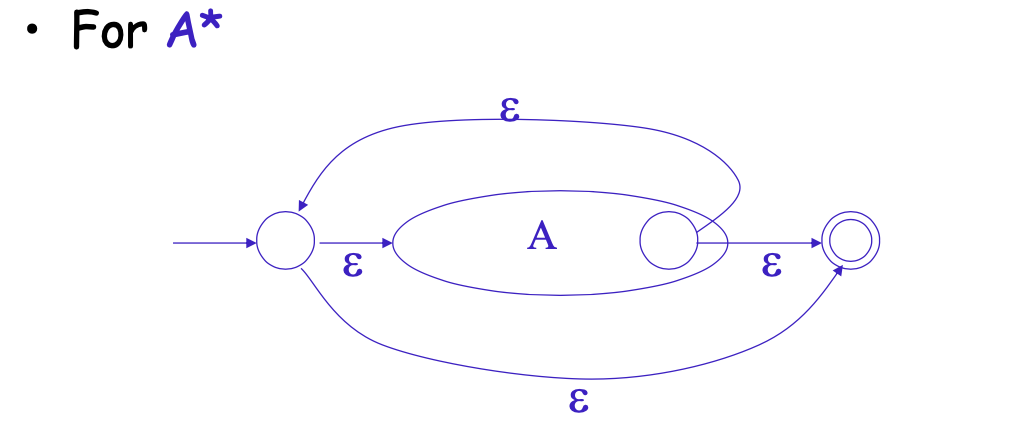
然后对于正则的几种表达式， 都可以进行转换，并通过上述的M结构进行嵌套使用

image-20220210205544857

image-20220210205554613

# e-closure

epsilon闭包，

e-closure(P)指从P开始， 可以通过e-moves到达的状态的集合。

# 从NFA到DFA

  • 确定DFA起始状态

    • E-closure(NFA-start-state) 作为DFA的起始状态

  • 然后开始增加 S -a-> S'的变换，

    • S'是S中的每个状态接收到a元素后变化的集合，这个结果也包含可以通过e-moves到达的状态。

  • 不断进行状态更新，知道计算出所有状态对所有输入的关系，即可得到DFA

# Table-driven: DFA的实现

DFA的概念可以通过二维的表进行实现，

因为DFA所有的节点间关系都可以通过 S1 --a--> S2表示，因此我们可以通过 state-input symbol二维表表示整个DFA， 这个关系可以表示为 Table[S1, a] = S2;

那么接受输入并进行状态切换我们只需要进行一个简单的查表操作即可。十分高效。

state = Table[state, sym];
1

# 对于实现而言的问题

emmmm 太数学化了， 仔细考虑下， 其实我对于这个有限状态机的实现最开始的想法就是 while-switch， 其实就是一个简单的abstract machines， 都可以通过while-switch进行实现。

看到一些大佬们的讨论，

为什么很多语言的实现里面的 Lexer 都没有使用 DFA？ (opens new window)

基于表驱动实现的词法分析的一点疑问？ (opens new window)

词法解析具体过程怎样，完全通过正则吗？ (opens new window)

一个automata的实现形式：

  • 代码位置隐含
  • Switch-case 控制state变量
  • table-based

# 代码位置隐含

这个并没有看到具体的例子，大部分应该是手写出来的， 自己实现出来的，没有显示的state变量，但是由于程序逻辑上仍然是automata的实现思路。

# switch-case

应该是最符合直觉的实现，大概样子是

state = start_state 
while (next =next_input()){
	switch(state){
			case case_of_state:
					switch(next) {
							case case_of_input:
									..transition : state = next_state 
					}
	}
}
1
2
3
4
5
6
7
8
9
10

最外层是while一致进行读取，

其次是switch分类不同的状态，

然后在不同状态之下， 又一层switch分类此状态接受不同输入后进行的状态变化。

# table-based

其实switch和table是对应的，单层switch完全可以通过一个table进行实现，在汇编层的优化中也经常出现这种情况。

对应上面我们提到的while-switch-switch的形式，对应的table应该是 while-table[state][input]的实现。

# 比较

三种实现方案的比较。应该是以switch-case最为简单，table-based运行效率可能会高一些，

但是对于某些词法比较简单(cpython lua)和词法复杂(ruby)的情况，一般都是手写。

上次更新: 6/24/2025, 5:07:55 AM
Theme by Vdoing | Copyright © 2019-2025 lingze | MIT License